比较排序研究

今天在BYR论坛算法版看到一个关于比较排序的问题。题目很经典，如下：给你n个互不相同的数，最少用多少次比较可以完全确定各个数的大小关系。也就是问基于比较的排序最少比较次数是多少？

网上大多数人都是用信息论的思想去理解。这种想法是很好的，不过完全可以正宗的离散数学方法来解决这个问题。下面我给出结果以及证明。

设 表示将n个互不相同的数（其实相同也没关系，这里是为了让读者更容易理解）排序需要的最少比较次数。

设这n个数是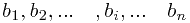  

我们经过m次比较操作确定了每个数之间的关系，记这m次操作如下：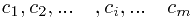

因为比较操作都是独立的，并不互相影响，所以改变它们的次序对结果无任何影响。我们把所有牵涉到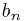的比较操作都往后移，那么前面的与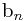无关的比较操作肯定确定了 的大小关系，也就是前n-1个数已经排好顺序了。现在只要确定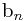在这个排列中的位置就可以了，肯定是用二分查找最快。所以我们可以得到下面的第推式（a字母怎么有两种写法，哪位朋友知道怎么解决吗？）：

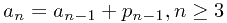                               变换一下得到

           

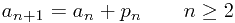
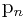表示往一个含有n个元素的有序排列中插入一个新的元素，并且保证排列仍然有序，所需要的最少比较次数。很多人会认为是 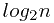， 这显然是错误的，因为它可能会得出小数。所以我们要用取整函数要进行调整，我试了下，发现上取整函数、下取整函数都不行，所以我们要发明一个新的取整函 数，我称之为 SuperCeil（超级上取整函数），它和ceil（上取整函数）有点儿像，比如 SuperCeil(1.23) = 2，SuperCeil(2.345) = 3，SuperCeil(7.00001) = 8。但是对整数的处理不一样，ceil(3) = 3，而 SuperCeil(3) = 4；SuperCeil(5) = 6。我想大家应该明白了SuperCeil的意义。这样我们就得到了最终的结果：

          

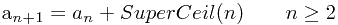
           初始条件是 ， 因为两个数显然比较一次就可以了。


OK，问题应该算解决了，但是还不太严密。关于如何求这个第推式的通项，我还没想出来。先放在此博客上如果您有方法求解，或者发现了错误，请在此博客留言或用邮件通知我。